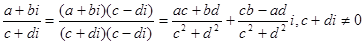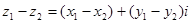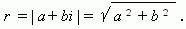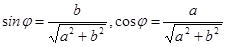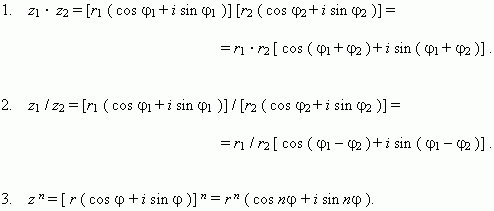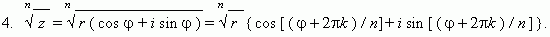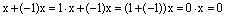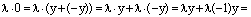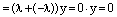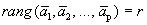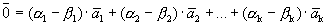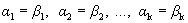что такое поле комплексных чисел
Поле комплексных чисел
Рассмотрим важнейший пример числового поля — поле комплексных чисел.
Два комплексных числа и называются равными, если равны их действительные и мнимые части соответственно:
Сложение и вычитание в поле комплексных чисел
Суммой комплексных чисел и называется комплексное число
Из этого определения и свойств операции сложения действительных чисел следует, что:
а) операция сложения комплексных чисел коммутативна: ;
б) операция сложения комплексных чисел ассоциативна: ;
в) существует нулевой элемент ; нулевой элемент обозначается просто символом нуль ;
г) для каждого комплексного числа существует противоположный ему элемент
Из последнего свойства следует, что на множестве комплексных чисел определена операция вычитания (обратная к сложению). Разностью чисел и называется комплексное число
Умножение и деление в поле комплексных чисел
Произведением комплексных чисел и называется комплексное число
Из определения (В.6) и свойств операции умножения действительных чисел следует, что:
в) существует единичный элемент ; единичный элемент обозначается просто символом единица: ;
Из последнего свойства следует, что на множестве отличных от нуля комплексных чисел определена операция деления (обратная к умножению).
Частным двух чисел и называется комплексное число
Операции сложения и умножения комплексных чисел связаны законом дистрибутивности:
Таким образом, множество комплексных чисел является полем.
Решение. По определению операций получаем
Сопряженные числа в поле комплексных чисел
Из определения следует, что сумма и произведение сопряженных чисел — есть числа действительные:
Используя правила арифметических операций для комплексных чисел, можно установить справедливость свойств операции комплексного сопряжения:
Решение. Пусть — корень уравнения. Тогда
Приравнивая нулю действительную и мнимую части, получаем
3. Из свойств операции комплексного сопряжения следует, что
Поле комплексных чисел



Теорема 1. Множество комплексных чисел С с операциями сложения и умножения образует поле. Свойства сложения
1) Коммутативность:(a+bi)+(c+di)=(a+c)+(b+d)i=(c+di)+(a+bi).
2) Ассоциативность :[(a+bi)+(c+di)]+(e+fi)=(a+c+e)+(b+d+f)i=(a+bi)+[(c+di)+(e+fi)].
3) Существование нейтрального элемента:(a+bi)+(0+0i)=(a+bi). Число 0+0i будем называть нулём и обозначать 0.
4) Существование противоположного элемента: (a+bi)+(–a–bi)=0+0i=0.
5) Коммутативность умножения: (a+bi)(c+di)=(ac–bd)+(bc+ad)i=(c+di)(a+bi).
6) Ассоциативность умножения:если z1=a+bi, z2=c+di, z3=e+fi, то (z1z2)z3 =z1(z2z3).
7) Дистрибутивность: если z1=a+bi, z2=c+di, z3=e+fi, то z1(z2+z3)=z1z2+z1z3.
8) Нейтральный элемент для умножения:(a+bi)(1+0i)=(a·1–b·0)+(a·0+b·1)i=a+bi.
9) Число 1+0i=1 – единица.
Если b=0, то z=a+ 0i=a– действительное число. Поэтому множество действительных чисел Rявляется частью множества комплексных чисел C: R Í C.
Заметим: i 2 =(0+1i)(0+1i)=–1+0i=–1. Используя это свойство числа i, а также свойства операций, доказанные в теореме 1, можно выполнять действия с комплексными числами по обычным правилам, заменяя i 2 на –1.
2 Тригонометрическая форма записи.
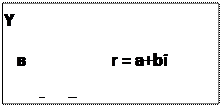



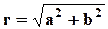
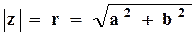
Полярный угол j называется аргументом числа z: 
Аргумент определяется с точностью до слагаемого 2kp; значение, для которого –p
Комплексные числа
Формы
Так сложилось в математике, что у данных чисел несколько форм. Число одно и тоже, но записать его можно по-разному:
Далее с примерами решений вы узнаете как переводить комплексные числа из одной формы в другую путем несложных действий в обе стороны.
Изображение
Изучение выше мы начали с алгебраической формы. Так как она является основополагающей. Чтобы было понятно в этой же форме изобразим комплексное число на плоскости:
Вычислить сумму и разность заданных комплексных чисел:
Сначала выполним сложение. Для этого просуммируем соответствующие мнимые и вещественные части комплексных чисел:
Аналогично выполним вычитание чисел:
Выполнить умножение и деление комплексных чисел:
Так, теперь разделим первое число на второе:
Суть деления в том, чтобы избавиться от комплексного числа в знаменателе. Для этого нужно домножить числитель и знаменатель дроби на комплексно-сопряженное число к знаменателю и затем раскрываем все скобки:
Разделим числитель на 29, чтобы записать дробь в виде алгебраической формы:
Для возведения в квадрат достаточно умножить число само на себя:
Пользуемся формулой для умножения, раскрываем скобки и приводим подобные:
В этом случае не всё так просто как в предыдущем случае, когда было возведение в квадрат. Конечно, можно прибегнуть к способу озвученному ранее и умножить число само на себя 7 раз, но это будет очень долгое и длинное решение. Гораздо проще будет воспользоваться формулой Муавра. Но она работает с числами в тригонометрической форме, а число задано в алгебраической. Значит, прежде переведем из одной формы в другую.
Вычисляем значение модуля:
Найдем чем равен аргумент:
$$ \varphi = arctg \frac<3> <3>= arctg(1) = \frac<\pi> <4>$$
Записываем в тригонометрическом виде:
Преобразуем в алгебраическую форму для наглядности:
Представим число в тригонометрической форме. Найдем модуль и аргумент:
Используем знакомую формулу Муавра для вычисления корней любой степени:
Поле комплексных чисел. Геометрическое представление комплексных чисел и операции над ними. Тригонометрическая форма комплексного числа
Комплексным числом zназ. выражение 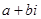
При этом выполняются соглашения:
1) с выражением a+bi можно производить арифметические операции по правилам, которые приняты для буквенных выражений в алгебре;
5) равенство a+bi=c+di, где a, b, c, d – действительные числа, имеет место тогда и только тогда, когда a=c и b=d.
Число 0+bi=bi называется мнимым или чисто мнимым.
Любое действительное число а есть частный случай комплексного числа, ведь его можно записать в виде a=a+ 0i. В частности, 0=0+0i, но тогда ели a+bi=0, то a+bi=0+0i, следовательно, a=b=0.
Т.о., комплексное число a+bi=0 тогда и только тогда, когда a=0 и b=0.
Из соглашений следуют законы преобразования комплексных чисел:
Мы видим, что сумма, разность, произведение и частное (где делитель не равен нулю) комплексных чисел, в свою очередь комплексное число.
Число а наз. вещественной частью комплексного числа z (обозначается 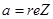
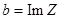
Комплексное число z с нулевой вещественной частью наз. чисто мнимым, с нулевой мнимой – чисто вещественным.
Два комплексных числа наз.равными,если у них совпадают и вещественная и мнимая части.
Два комплексных числа наз. сопряженными, если у них веществ. части совпадают, а мнимые отличаются знаками. 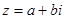
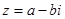
Сумма сопряженных чисел есть число веществ, а разность чисто мнимое число. На множестве комплексных чисел естественным образом определены операции умножения и сложения чисел. Именно, если 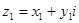
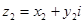
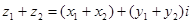
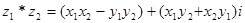
Определим теперь операции вычитания и деления.
Заметим, что произведение двух комплексных чисел есть число веществ.
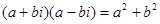
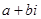
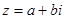
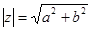
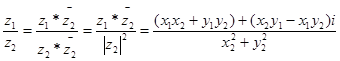
В отличие от вещественных чисел для комплексных чисел не вводится понятие «больше», «меньше».
Геометрическое представление комплексных чисел.Действительные числа изображаются точками на числовой прямой:
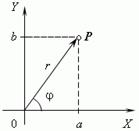
Здесь точка A означает число –3, точка B – число 2, и O – ноль. В отличие от этого комплексные числа изображаются точками на координатной плоскости. Выберем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на обеих осях. Тогда комплексное число a+ bi будет представлено точкой Р с абсциссой а и ординатой b (рис.). Эта система координат называется комплексной плоскостью.
Модулемкомплексного числа называется длина вектора OP, изображающего комплексное число на координатной (комплексной) плоскости. Модуль комплексного числа a+ bi обозначается | a+ bi | или буквой r и равен:
Сопряжённые комплексные числа имеют одинаковый модуль. __
Тригонометрическая формакомплексного числа. Наряду с записью комплексного числа в алгебраической форме также употребляется и другая, называемая тригонометрической.
Пусть комплексное число z=a+bi изображается вектором ОА с координатами (a,b). Обозначим длину вектора ОА буковой r: r=|ОА|, а угол, который он образует с положительным направлением оси Ох – через угол φ.
Воспользовавшись определениями функций sinφ=b/r, cosφ=a/r, комплексное число z=a+bi можно записать в виде z=r(cosφ+i*sinφ), где 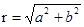
Тригонометрической формой комплексного числа z называется его представление в виде z=r(cosφ+i*sinφ), где r и φ – действительные числа и r≥0.
Действительно число r называется модулем комплексного числа и обозначается |z|, а угол φ – аргументом комплексного числа z. Аргумент φ комплексного числа z обозначается Arg z.
Операции с комплексными числами, представленными в тригонометрической форме:
Это знаменитая формула Муавра.
8.Векторное пространство. Примеры и простейшие свойства векторных пространств. Линейная зависимость и независимость системы векторов. Базис и ранг конечной системы векторов
Для векторов трёхмерного пространства указаны правила сложения векторов и умножения их на действительные числа. В применении к любым векторам х, у, z и любым числам α, β эти правила удовлетворяют следующим условиям:
3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условию x+0=x: для любого вектора x;
4) для любого вектора х существует противоположный ему вектор у такой, что х+у =0,
6) α(βx)=(αβ)х (ассоциативность умножения), где произведение αβ есть произведение скаляров
7) (α+β)х=αх+βх (распределительное свойство относительно числового множителя);
8) α(х+у)=αх+αу(распределительное свойство относительно векторного множителя).
Векторным (или линейным) пространством называется множество R, состоящее из элементов любой природы (называемых векторами), в котором определены операции сложения элементов и умножения элементов на действительные числа, удовлетворяющие условиям 1-8.
Примерами таких пространств могут служить множество действительных чисел, множество векторов на плоскости и в пространстве, матрицы и т.д.
Теорема “Простейшие свойства векторных пространств”
1. В векторном пространстве существует единственный нулевой вектор.
2. В векторном пространстве любой вектор имеет единственный противоположный ему.
3. 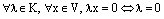
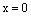
4. 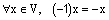
Док-во
Пусть 0 – нулевой вектор векторного пространства V. Тогда 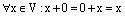
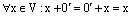
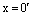
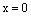
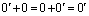
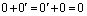
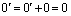
Сначала мы докажем, что произведение нулевого скаляра на любой вектор равен нулевому вектору.
Пусть 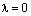
Относительно сложения векторное пространство является абелевой группой, а в любой группе справедлив закон сокращения. Применяя закон сокращения, из последнего равенства следует 0*х=0
Теперь докажем утверждение 4). Пусть 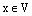
Отсюда сразу же следует, что вектор (-1)х является противоположным вектору х.
Пусть теперь х=0. Тогда, применяя аксиомы векторного пространства, 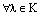

Пусть 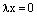
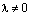
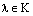
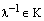
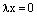
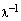
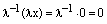
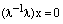
Линейная зависимость и независимость системы векторов. Набор векторов 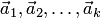
Система из 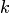
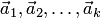
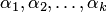
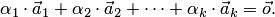
Система из k векторов 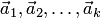
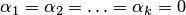
Замечания:
1. Один вектор 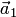
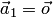
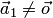
2. Любая часть системы векторов называется подсистемой.
Свойства линейно зависимых и линейно независимых векторов:
1. Если в систему векторов входит нулевой вектор, то она линейно-зависима.
2. Если в системе векторов имеется два равных вектора, то она линейно-зависима.
3. Если в системе векторов имеется два пропорциональных вектора 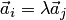
4. Система из k>1 векторов линейно-зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.
5. Любые векторы, входящие в линейно-независимую систему, образуют линейно-независимую подсистему.
6. Система векторов, содержащая линейно-зависимую подсистему, линейно-зависима.
7. Если система векторов 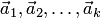
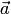
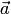
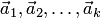
Тогда из равенства 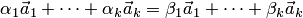
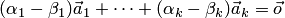
Следовательно, линейная комбинация векторов 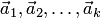
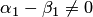
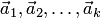
Ранг и базис системы векторов. Рангом системы векторов называется максимальное число линейно-независимых векторов системы.
Базисом системы векторов называется максимальная линейно независимая подсистема данной системы векторов.
Теорема. Любой вектор системы можно представить в виде линейной комбинации векторов базиса системы. (Всякий вектор системы можно разложить по векторам базиса.) Коэффициенты разложения определяются для данного вектора и данного базиса однозначно.
Док-во:
Пусть система 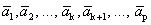
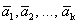
1 случай. Вектор 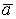
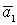
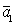
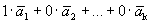
2 случай. Вектор 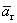
Рассмотрим систему векторов 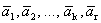
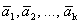
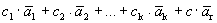
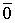
Очевидно, что 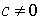
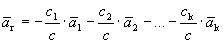
Докажем, что разложение вектора по базису единственно. Предположим противное: имеется два разложения вектора по базису.
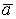
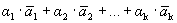
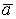
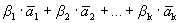
Вычитая эти равенства, получим
Учитывая линейную независимость векторов базиса, получим
Следовательно, разложение вектора по базису единственно.
Количество векторов в любом базисе системы одинаково и равно рангу системы векторов.